The Challenges of 3D to 2D Flattening

Validation of accurate and fast 3D to 2D flattening is a key requirement when considering the transition to digital pattering software. Good results are dependent on the implementation of several factors. This article provides a discussion of some of the most important factors.

The initial Tessellation (meshing) of the 3D design

Before a 3D CAD model can be flattened into a 2D pattern, the 3D design must be converted into a 3D mesh. Meshing or Tessellation is a mathematical process used to represent the surfaces of the initial design model as a series of polygons (triangles) with no gaps.

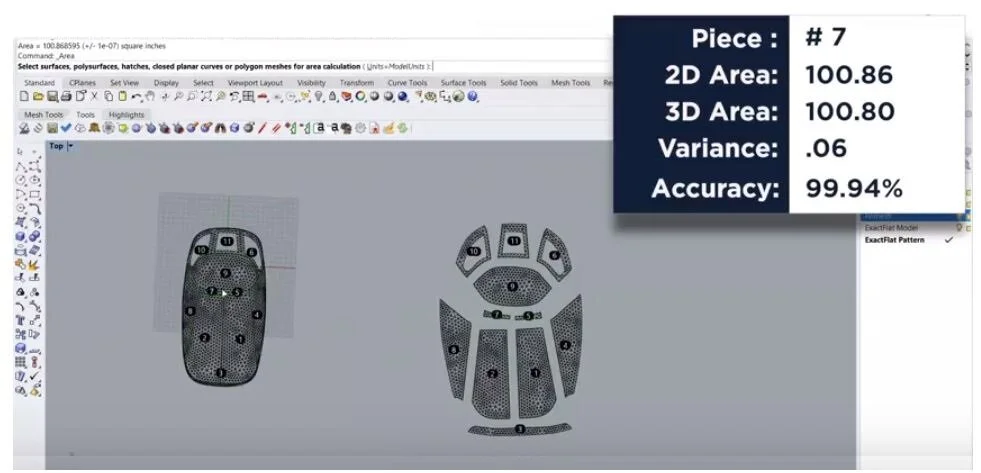
One thing to note is that the perimeter lengths of edges on the surface files vs. the lengths of the same edges calculated with tessellated meshes may vary. This is due to the representation of those edges as curves, arcs or splines for the surfaces files vs. polylines for the tessellated meshes. Also, of concern is the density of the mesh, which is represented by the number of mesh polygons, as well as the shape of the mesh polygons. See the shapes below for examples.

The image shows the sample model with varying degrees of tessellation. Mesh tools within the CAD package are used to convert the 3D design model into a format ready for flattening. Several conversion factors affect the margin of error between the de… — The image shows the sample model with varying degrees of tessellation. Mesh tools within the CAD package are used to convert the 3D design model into a format ready for flattening. Several conversion factors affect the margin of error between the design model and the mesh

Mesh Quality

Click on the image to see how in ideal mesh for flattening is created

The goal of the initial tessellation is to represent the design with a minimum amount of error. In most applications, surfaces are converted into a tessellated mesh by the 3D CAD programs. The meshes created by native CAD programs are not always optimal for flattening. The latest generation of 3D flattening software products provide integrated remeshing tools. These tools are used to create a quality mesh which decreases flattening solve time and increases pattern accuracy. Good quality meshes are characterized by:

models with no more than 5,000 triangles,
six(6) triangles per vertex,
an aspect ratio of adjacent edges of 1-1,
a typical angle between the triangle edges of 60 degree.
uniform triangle size and density throughout the mesh

The ideal polygon is an isosceles triangle.

Flattening Algorithms

3D flattening software creates 2D pieces by first reformatting the triangles on a flat surface. Depending on surface complexity and fabric material type, different algorithms are used for this step. Most 3D flattening tools employ some combination of the following types of algorithms

Linear Isotropic algorithms
Linear Orthotropic algorithms,
Load Ratio algorithms (load to stress ratio),
Cubic Orthotropic algorithms,
Quintic Orthotropic algorithms.

To learn more

In the next article we'll evaluate the impact of a series of additional 3D flattening capabilities including Strain relief feedback, precise material properties and software performance. It is the combination of these factors that ensures the quality of the resulting patterns and the time savings achieved by ExactFlat clients.

To gain a better understanding of the tools and advantages of ExactFlat click on the link below and schedule a time to speak with one of our experts. ExactFlat, the solution for fast, accurate 3D to 2D flattening.